4
 Statistic Three:
The standard deviation (SD)
is an attempt to capture the distribution of scores (in a standardized way;
visually, the normal curve in the prior post). The 22 scores in the Nursing124
data (Tables 2 and 3) have been sorted only to make the charts easier to follow
(Chart 10).
Statistic Three:
The standard deviation (SD)
is an attempt to capture the distribution of scores (in a standardized way;
visually, the normal curve in the prior post). The 22 scores in the Nursing124
data (Tables 2 and 3) have been sorted only to make the charts easier to follow
(Chart 10).[Check Table 4 below, (PUP 5.20, Table 3c. Guttman Mark Matrix with Scores and Item Difficulty), for the values being plotted.]
[A Guttman table has the student scores sorted from high to
low, vertically, and item difficulties sorted high to low, horizontally. The
most difficult item and the lowest scoring student end up at the lower right
corner of the table.]
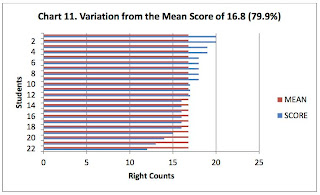 The variation in the student scores is readily visible when
the average score is added to the chart (Chart 11). It is this region of
variation that is captured by the standard deviation (SD). You can add or
subtract a constant number from every student score without changing the
variation.
The variation in the student scores is readily visible when
the average score is added to the chart (Chart 11). It is this region of
variation that is captured by the standard deviation (SD). You can add or
subtract a constant number from every student score without changing the
variation.
The deviation of each score from the average test score (the
mean) is extracted from the scores and is plotted next (Chart 12). These values
add to zero. The solution to this problem (back when this was all done with
paper and pencil) was to square the deviations. Now the numbers being used to
capture the variation in the scores are all positive and can be added (Chart
13). The sum of squares (SS) is 89.86.
About ½ of the SS is produced by just 3 of the most extreme
scores out of the 22 total. It is a matter of personal judgment when to call an
extreme score an outlier and remove it from further statistical analysis.
The calculation of the SD involves three steps shown on the
right side of the Guttman table (Table 4): the sum of squared deviations (SS)
[89.86], the mean of the sum of squares (Mean SS, MSS or Variance) [4.28], and
the SD (Square Root of the Mean SS or the Variance) [2.07]. Each step has been
given a name as in many calculations the SS or the Mean SS is used rather than
developing the SD and then reversing the process as needed.
 Standard here means done in a standardized way. The standard
is that 2/3 (68.3%) of the student scores and item difficulties are expected to
fall within the range of (+-) one SD of their average values. And 95.4% are
expected to fall within the range of (+-) two SDs of their average values.
Standard here means done in a standardized way. The standard
is that 2/3 (68.3%) of the student scores and item difficulties are expected to
fall within the range of (+-) one SD of their average values. And 95.4% are
expected to fall within the range of (+-) two SDs of their average values.
This standard generates the normal curve of error
that in education is shortened to the normal curve or bell curve
with both the meaning and use reversed. In the sciences and engineering, error
is to be avoided. In education, error is used to produce the spread of scores
needed to assign letter grades in schools designed for failure and to assign
the pass/fail point on NCLB standardized assessments.
[This need for a wide distribution of scores for setting
test grades may result in problems in establishing the precision of student
scores. This needs to be checked when I get to the standard error of
measurement, statistic #5, in this series.]
The above calculations are shown for N and for N – 1 when
calculating the Mean SS. N – 1 is a correction for classroom sized test data,
when the number of students and questions is below 100.
Table 4 shows the SD for student scores and for item
difficulties. Item difficulties generally have a wider spread (3.17), a larger
SD, than student scores (2.07) in classroom tests.
I have fully developed Table 4, Standard Deviation (SD) Calculations, as this shows the foundation for all of the remaining statistics in this series. The sum of squared deviations (SS) is 89.86 for student scores and 201.40 for item difficulties. Then dividing SS by the number summed produces the Mean SS or Variance. The square root of the Mean SS is the SD. This is totally reversible. Square the SD yields the Mean SS. Multiply the Mean SS by the number of summed to get back to the SS.
I have fully developed Table 4, Standard Deviation (SD) Calculations, as this shows the foundation for all of the remaining statistics in this series. The sum of squared deviations (SS) is 89.86 for student scores and 201.40 for item difficulties. Then dividing SS by the number summed produces the Mean SS or Variance. The square root of the Mean SS is the SD. This is totally reversible. Square the SD yields the Mean SS. Multiply the Mean SS by the number of summed to get back to the SS.
The above paragraph reports honest number manipulations. There is no room for bias in calculating the SS. However, the deviations squared (DEVSQR) are spread over a wider range than the actual deviations. A large SD can be due to an evenly distributed set of scores or to a narrow distribution with one or more outliers far from the average score. Two identical SDs may result from two very different distributions.
This can be a problem in classroom tests. Standardized tests reduce the problem by sampling a large enough number of students or items to get a stable distribution.
[The SS are also used in the analysis of variance (ANOVA) commonly used in the sciences and engineering. I never saw it used in education when I was teaching. The ANOVA permits one to determine if the distribution of marks in rows and columns is just a matter of luck or if there is something else at play. If the null hypothesis, that the distribution is no different than a matter of luck, holds, there is then no need to do any other statistical tests.
 The calculations (in yellow) for the ANOVA have been added
to the left and bottom edge of Table 4. The grand mean is 0.779 (based on the
values of right and wrong marks, 1 and 0). The deviations squared (DEVSQR) for
each score and difficulty are listed in respect to the grand mean. The total
degrees of freedom is the count of cells in the table minus 1 (462 – 1).
The calculations (in yellow) for the ANOVA have been added
to the left and bottom edge of Table 4. The grand mean is 0.779 (based on the
values of right and wrong marks, 1 and 0). The deviations squared (DEVSQR) for
each score and difficulty are listed in respect to the grand mean. The total
degrees of freedom is the count of cells in the table minus 1 (462 – 1).
The ANOVA (Table 5) yields Mean SS ratio between student
score rows and unexplained (or error) within rows or between columns (0.20/0.16)
for an F test value of 1.27. This
value does not exceed the 5% level of significance F table for 21/440 degrees
of freedom critical value of 1.59. The variation found in this table of student
marks may be a matter of luck (student preparation and attitude, item authoring,
test creator item selection, testing environment, and pure chance).]
- - - - - - - - - - - - - - - - - - - - -
Free software to help you and your students experience and understand the change from TMC to KJS (tricycle to bicycle):



I'm happy to find numerous useful info here in the post. I would really like to come back again right here for likewise good articles or blog posts. Thanks for sharing..
ReplyDeleteTop MBA Colleges in Pune
MBA Institutes in Pune
Thank you for your comment.
ReplyDelete